机器学习笔记(一):模型评估与选择
目录
经验误差与过拟合
错误率:分类错误的样本数占样本总数的比例。m个样本中有a个样本分类错误,则错误率E=a/m。
精度:分类正确的样本数占样本总数的比例。精度=1-错误率。
误差:学习器实际预测的输出与样本的真实输出之间的差异。训练集上的误差称为“训练误差”或“经验误差”,在新样本上的误差称为“泛化误差”。
过拟合:把训练样本自身的一些特点当做所有样本的一般性质,泛化性能下降。
欠拟合:对训练样本的一般性质尚未学好,学习能力过低。
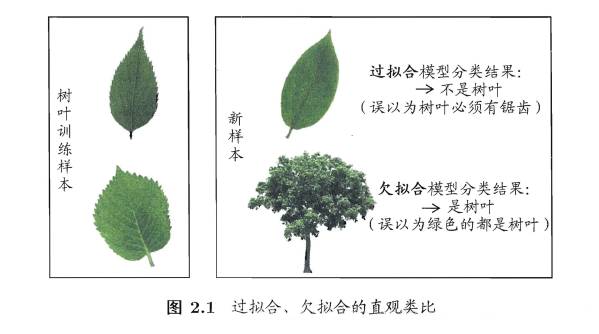
我们的目标是在新样本上表现好的学习器,即泛化误差小。当学习器把训练样本学的太好时,可能会出现过拟合情况。欠拟合比较容易客服,如增加训练轮数等,而过拟合是无法彻底避免的,只能缓解或者说减小其风险。
面对具体任务时,往往有多种算法可供选择,以及不同的参数配置。选择算法、配置参数的过程就叫做“模型选择”。理想的解决方案是对候选模型的泛化误差进行评估,选择泛化误差最小的模型。
评估方法
训练集:用来训练学习器的数据集。
测试集:用来测试学习器对新样本判别能力的数据集。在测试集上的“测试误差”将作为泛化误差的近似。测试集应尽可能与训练集互斥。
现有包含m个样例的数据集D={(x1,y1), (x2,y2), …, (xm,ym)},既要训练又要测试,将D分为训练集S和测试T。
